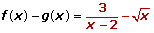UNIDAD 3 Y 4

Calculo Diferencial

Unidad III - IV

Unidad III: Limites y Continuidad

LIMITE DE UNA SUCESION

Eventualmente todos los elementos de la sucesión se aproximan tanto como 

queramos al valor límite. La condición que impone que los elementos se 

encuentren arbitrariamente cercanos a los elementos subsiguientes no implica, 

en general, que la sucesión tenga un límite.

El límite de una sucesión es el número al cual se van aproximando 

los términos de una sucesión.

  a₁= 1                               

a₂= 0.5                         

a₁₀₀₀= 0.001               

a_{1000 000} = 0.000001

El límite es 0.           

LIMITE DE UNA FUNCION DE VARIABLE REAL

Se le llama función real de variable real a toda la función definida de un 

subconjunto D de los números reales, en el conjunto R de los números reales, 

tal que a cada elemento x de D le corresponde uno y sólo un elemento y de R:

f:D————->R

x————->x2.

Para que una función quede correctamente definida 

es necesario determinar: 

~El conjunto inicial o dominio de la función. 

~El conjunto final o imagen de la función. 

~La regla por la cual se asigna a cada elemento del conjunto 

origen un solo elemento del conjunto imagen. 

Así, por ejemplo, la función definida por:

f:R ——–>R

x———>x2.

CALCULO DE LIMITES

Si f(x) es una función usual (polinómicas, racionales, radicales, 

exponenciales, logarítmicas, etc.) y está definida en el punto a, 

entonces se suele cumplir que:

Es decir: Para calcular el límite se sustituye en

 la función el valor al que tienden las x.

No podemos calcular porque el dominio de definición está en el intervalo [0, ∞), por tanto no puede tomar valores que se acerquen a -2.

PROPIEDADES DE LOS LIMITES

Las Propiedades de los límites implican operaciones que se pueden emplear con el fin de simplificar el límite de una función y convertirlos en una forma mucho más sencilla. Estas propiedades pueden utilizarse con el fin de encontrar los límites de las combinaciones de dos o más funciones o para demostrar si el límite de la función existe o no.

Cuando se trata con la combinación de dos o más funciones, por lo general, los límites de las funciones se calculan individualmente, con la ayuda de estas propiedades, y por último combinando estos con el fin de llegar al resultado final.

Estas propiedades expresan que el resultado será el mismo si el límite es tomado primero y después se realiza el álgebra o realizando el álgebra primero y luego tomando los límites.

- See more at: http://mitecnologico.com/igestion/Main/PropiedadesDeLosLimites#sthash.HsY3niTd.dpuf

Las Propiedades de los límites implican operaciones que se pueden emplear con el fin de simplificar el límite de una función y convertirlos en una forma mucho más sencilla. Estas propiedades pueden utilizarse con el fin de encontrar los límites de las combinaciones de dos o más funciones o para demostrar si el límite de la función existe o no.

Cuando se trata con la combinación de dos o más funciones, por lo general, los límites de las funciones se calculan individualmente, con la ayuda de estas propiedades, y por último combinando estos con el fin de llegar al resultado final.

Estas propiedades expresan que el resultado será el mismo si el límite es tomado primero y después se realiza el álgebra o realizando el álgebra primero y luego tomando los límites.

- See more at: http://mitecnologico.com/igestion/Main/PropiedadesDeLosLimites#sthash.HsY3niTd.dpufLas Propiedades de los límites implican operaciones que se pueden emplear con el fin de simplificar el límite de una función y convertirlos en una forma mucho más sencilla. Estas propiedades pueden utilizarse con el fin de encontrar los límites de las combinaciones de dos o más funciones o para demostrar si el límite de la función existe o no.


Cuando se trata con la combinación de dos o más funciones, por lo general, los límites de las funciones se calculan individualmente, con la ayuda de estas propiedades, y por último combinando estos con el fin de llegar al resultado final.




Estas propiedades expresan que el resultado será el mismo si el límite es tomado primero y después se realiza el álgebra o realizando el álgebra primero y luego tomando los límites.


Las Propiedades de los límites implican operaciones que se pueden emplear con el fin de simplificar el límite de una función y convertirlos en una forma mucho más sencilla. Estas propiedades pueden utilizarse con el fin de encontrar los límites de las combinaciones de dos o más funciones o para demostrar si el límite de la función existe o no.

Cuando se trata con la combinación de dos o más funciones, por lo general, los límites de las funciones se calculan individualmente, con la ayuda de estas propiedades, y por último combinando estos con el fin de llegar al resultado final.

Estas propiedades expresan que el resultado será el mismo si el límite es tomado primero y después se realiza el álgebra o realizando el álgebra primero y luego tomando los límites. - See more at: http://mitecnologico.com/igestion/Main/PropiedadesDeLosLimites#sthash.HsY3niTd.dpuf

Las propiedades de los límites implican operaciones que se pueden 

emplear con el fin de simplificar el límite de una función y convertirlos 

en una forma mucho más sencilla. Estas propiedades pueden utilizarse 

con el fin de encontrar los límites de las combinaciones de dos o más 

funciones o para demostrar si el límite de la función existe o no.

Cuando se trata con la combinación de dos o más funciones, por lo 

general, los límites de las funciones se calculan individualmente, con la 

ayuda de estas propiedades, y por último combinando estos con el fin de 

llegar al resultado final.

Estas propiedades expresan que el resultado será el mismo si el límite 

es tomado primero y después se realiza el álgebra o realizando el 

álgebra primero y luego tomando los límites.

EJEMPLOS:

Límite de una constante

Límite de una suma

Límite de un producto

Límite de un cociente

Límite de una potencia

Límite de una función

g puede ser una raíz, un log, sen ,cos, tg, etc. 

Límite de una raíz

Límite de un logaritmo

LIMITES LATERALES

El límte lateral por la derecha de una función y = f(x) en el punto x = a 

es el valor al que se aproxima f(x) cuando x se aproxima al valor de a 

por valores mayores que a.

El límite lateral por la izquierda de una función y=f(x) en el punto x = a 

es el valor al que se aproxima f(x) cuando x se aproxima al valor de a 

por valores menores que a.

LIMITES INFINITOS Y LIMITES AL INFINITO

Si una variable independiente x está creciendo indefinidamente através 

de valores positivos se escribe 

y si decrece a través de valores negativos se denota como 

Similarmente cuando una funcion f(x) crece indefinidamente y toma 

valores positivos cada vez mayores, es escribe ƒ(x)→ + ∞ y si decrece 

tomando valores negativos se escribe ƒ(x)→ – ∞.

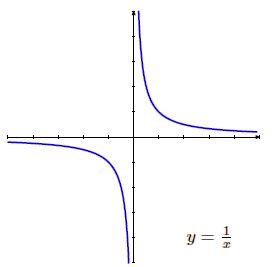
ASINTOTAS

Una línea recta que se aproxima continuamente a otra función o 

curva, que la distancia entre las 2 tiende a 0 a medida que 

se extiende indefinidamente. 

También se puede decir que es la curva la que se aproxima 

continuamente a la recta, o que en ambas presentan 

un comportamiento asintótico.

FINCIONES CONTINUAS Y DISCOTINUAS EN 

UN PUNTO Y EN UN INTERVALO

CONTINUA

Una función es continua en un punto si existe límite en él y coincide 

con el valor que toma la función en ese punto.

Una idea intuitiva de función continua se tiene al considerar que su 

gráfica es continua, en el sentido que se puede dibujar sin levantar 

el lápiz de la hoja de papel.

Continuidad de una función en un punto

Se dice que una función f(x) es continua en un punto x = a si y sólo 

si se cumplen las tres condiciones siguientes:

1. Que el punto x= a tenga imagen.

2. Que exista el límite de la función en el punto x = a.

3. Que la imagen del punto coincida con el límite de la función en el punto.

Si una función no es continua en un punto x=a, 

diremos que es discontinua en dicho punto.

DISCONTINUA

1.- Una función es discontinua en un punto cuando no existe límite en

 él o, existiendo, no coincide con el valor de la función en el mismo. 

2.- Una función tiene una discontinuidad evitable en un punto cuando 

existe límite en él y no coincide con el valor de la función en el mismo.

 El valor que deberíamos dar a la función en dicho punto para que fuera 

continua en él se llama verdadero valor de la función en el mismo. 

3.- Una función tiene una discontinuidad inevitable.

TIPOS DE DISCONTINUIDAD

Discontinuidad evitable 

Si una función tiene límite en un punto, pero la función 

en ese punto tiene un valor distinto: 

o no existe: 

se dice que la discontinuidad es evitable, asignando a la función, 

en ese punto, el valor del límite: 

Discontinuidad esencial o no evitable 

Se dice que una función presenta una discontinuidad esencial 

cuando se produce algunas de las siguientes situaciones: 

~Existen los límites laterales pero no coinciden. 

~Alguno de los límites laterales o ambos son infinitos. 

~No existe alguno de los límites laterales o ambos. 

Discontinuidad de primera especie 

En este tipo de discontinuidad existen tres tipos: 

De salto finito 

Existen el límite por la derecha y por la izquierda del punto, su 

valor es finito, pero no son iguales: 

A este tipo de discontinuidad de primera especie se le llama salto finito, 

y el salto viene dado por: De salto infinitoSi uno de los límites laterales 

es infinito y el otro finito, tanto si el límite por la izquierda es finito 

y el de la derecha infinito: 

como en el caso de que el límite por la izquierda sea 

infinito y por la derecha finito: 

Se dice que la discontinuidad es de salto infinito. 

Discontinuidad asintótica 

Si los dos límites laterales de la función en el punto 

x= a son infinitos: 

A este tipo de discontinuidad de primera especie se le llama 

discontinuidad asintótica, siendo x= a la asíntota. 

Discontinuidad de segunda especie 

Si la función no existe en uno de los lados del punto, o no existen 

alguno, o ambos, de los límites laterales de la función en ese punto, 

se dice que la función presenta una discontinuidad de segunda 

especie en ese punto.

Unidad IV: Derivadas

CONSEPTO DE INCREMENTO Y RAZON DE CAMBIO. 

LA DERIVADA DE UNA FUNCION

 es un vector que apunta hacia la dirección donde la función ve un mayor incremento en su valor.

A la luz de la afirmación anterior se puede concluir que la derivada de la función es generalmente cero en algunos mínimos locales o máximos locales dado que en esa posición la función no notaincrementos hacia una dirección en particular.

En algunos lugares la palabra gradiente también se usa para denotar la derivada de la función.

Sin embargo, esta palabra es más apropiada para la derivada de la función de un vector o para una función con múltiples variables.

El símbolo griego delta, representado como un triángulo es utilizado para mostrar el cambio en el valor de una variable. y significaría un cambio en el valor de y.

La pendiente de una línea recta se puede calcular como

- See more at: http://mitecnologico.com/igestion/Main/ConceptosDeIncrementoYDeRazonDeCambioLaDerivadaDeUnaFuncion#sthash.YZylWewe.dpuf

 es un vector que apunta hacia la dirección donde la función ve un mayor incremento en su valor.

A la luz de la afirmación anterior se puede concluir que la derivada de la función es generalmente cero en algunos mínimos locales o máximos locales dado que en esa posición la función no notaincrementos hacia una dirección en particular.

En algunos lugares la palabra gradiente también se usa para denotar la derivada de la función.

Sin embargo, esta palabra es más apropiada para la derivada de la función de un vector o para una función con múltiples variables.

El símbolo griego delta, representado como un triángulo es utilizado para mostrar el cambio en el valor de una variable. y significaría un cambio en el valor de y.

La pendiente de una línea recta se puede calcular como

- See more at: http://mitecnologico.com/igestion/Main/ConceptosDeIncrementoYDeRazonDeCambioLaDerivadaDeUnaFuncion#sthash.YZylWewe.dpuf

La derivada de una función es un vector que apunta hacia la dirección 

donde la función ve un mayor incremento en su valor. 

A la luz de la afirmación anterior se puede concluir que la derivada 

de la función es generalmente cero en algunos mínimos locales o 

máximos locales dado que en esa posición la función no nota 

incrementos hacia una dirección en particular. 

La pendiente de una línea recta se puede calcular como: 

La expresión anterior se denomina como cociente de la diferencia. Esto se 

debe a que representa la diferencia entre dos cocientes.

La tasa o razón de cambio puede ser constante o no. Una tasa de cambio 

constante es aquella que no cambia durante un período de tiempo.

Como sabemos la variación en la tasa es un cociente de la diferencia, la 

tasa instantánea de cambio será el límite de esos cocientes.

La tasa de cambio instantánea es popularmente conocida 

por el nombre de derivada.

Ejemplo:

LA INTERPRETACION GEOMETRICA DE LA DERIVADA

Además de evaluar el valor de una función en cierto punto, también 

es esencial que evaluemos la variación en el valor de la función a medida 

que la entrada de la función varía. 

Esto se conoce como la pendiente de la recta en el caso de una recta 

lineal. Mientras que para una recta curva, la pendiente de la recta 

varía en cada punto.

 Esto significa que para una línea recta / función lineal se 

obtiene un número constante como su pendiente. Mientras que para una 

recta curva la pendiente es una función del valor de entrada de la funcion.

Supongamos que una función f(x) = x2. La gráfica de la función luciría 

de la siguiente forma:

La curva de color azul representa el gráfico de la función. Tome dos puntos 

en el eje x, supongamos x y x0 como en el gráfico de arriba. 

Determine el valor de la función en esos valores de x. Ahora trace una línea 

que pase por esos puntos sobre la curva de la función para obtener 

una línea recta.

A medida que muevo los puntos sobre el eje x más cerca uno del otro 

conseguimos una recta menos pronunciada que pasa a través de la curva 

de la función. En el instante que x = x0, la gráfica se vería así

CONCEPTO DE DIFERIENCIA, INTERPRETACION 

GEOMETRICA DE LOS DIFERENCIALES

El diferencial se puede tomar en el sentido geométrico como la elevación de 

la tangente desde el punto en que se toma el diferencial.

 

Recuérdese que la derivada de la función en el punto es la pendiente de la 

recta tangente a la función en el punto, como sabemos que la tangente de 

un ángulo es igual al cociente entre el cateto opuesto (incremento de y) 

y el cateto contiguo (incremento de x) de un hipotético triángulo rectángulo, 

sólo hay que despejar el incremento de y que equivale a nuestro diferencial.

 

Vista geométricamente, la elevación se produce verticalmente a partir 

del punto en que se toma el diferencial. El incremento que se tome 

representará el alejamiento horizontal que haga desde el punto en cuestión.

 

Así la elevación de la tangente que se obtenga como resultado dependerá 

del punto en cuestión y del alejamiento horizontal que se tomen, que 

en la formulas matemáticas están definidos respectivamente por y .

PROPIEDAD DE LA DERIVADA

Las derivadas forman una parte importante del cálculo. 

Hablando en términos sencillos, la derivada es una medida de la tasa de 

variación de la salida de una función así como varía la entrada de la función. 

En base a la definición anterior está claro que la salida de la función es 

una función de la entrada de la función. 

Las derivadas tienen algunas propiedades especiales que son importantes 

estudiar antes de saltar de lleno en el tema. 

Algunas de las propiedades más importantes son las siguientes: 

1. Si la función f(x): X → Y es diferenciable en un punto P, entonces se puede 

concluir que la función f(x) es continua en el punto p. 

2. La derivada de la suma de dos funciones es igual a la suma de las 

derivadas de las dos funciones tomadas individualmente. La misma regla 

aplica también para la resta de dos derivadas. Esta regla es más conocida 

por el nombre de la regla de la linealidad. 

3. La derivada de la multiplicación de una cantidad escalar con una 

función es igual a cuando la cantidad escalar se multiplica a la 

derivada de la misma función. 

4. La derivada de un número constante es siempre igual a cero. 

5. La diferenciación de una variable con respecto a si misma producirá uno. 

6. La derivada de la multiplicación de dos funciones es lo mismo que sumar la multiplicación de la primera función con la derivada de la segunda función y la multiplicación de la segunda función con la derivada de la primera función. Esta regla se conoce más comúnmente con el nombre de la regla del producto. 

7. La derivada de una variable elevada a una potencia es igual a las veces de 

la potencia de la derivada de la misma variable elevada a una potencia 

reducida por uno. Esta regla es mejor conocida por el nombre de la regla de la 

potencia. Es esencial que n sea un número real para que la propiedad 

anterior sea cierta. 

8. La derivada de la división de una función con alguna otra función 

es lo mismo que la división de la resta de la multiplicación de la primera

 función con la derivada de la segunda función y la multiplicación de la segunda 

función con la derivada de la primera función con el cuadrado de la segunda 

función. Aquí el valor de la función no debería ser igual a cero. Esta regla se 

conoce por el nombre de la regla del cociente. 

REGLA DE LA CADENA

la regla de la cadena es una fórmula para la derivada de la composición 

de dos funciones. Tiene aplicaciones en el cálculo algebraico de derivadas 

cuando existe composición de funciones. 

En términos intuitivos, si una variable y, depende de una segunda variable 

u, que a la vez depende de una tercera variable x; entonces, la razón de cambio 

de y con respecto ax puede ser calculada con el producto de la razón de cambio 

de y con respecto a u multiplicado por la razón de cambio de u con respecto a x.

Las Propiedades de los límites implican operaciones que se pueden emplear con el fin de simplificar el límite de una función y convertirlos en una forma mucho más sencilla. Estas propiedades pueden utilizarse con el fin de encontrar los límites de las combinaciones de dos o más funciones o para demostrar si el límite de la función existe o no.

Cuando se trata con la combinación de dos o más funciones, por lo general, los límites de las funciones se calculan individualmente, con la ayuda de estas propiedades, y por último combinando estos con el fin de llegar al resultado final.

Estas propiedades expresan que el resultado será el mismo si el límite es tomado primero y después se realiza el álgebra o realizando el álgebra primero y luego tomando los límites.

- See more at: http://mitecnologico.com/igestion/Main/PropiedadesDeLosLimites#sthash.HsY3niTd.dpuf

Las Propiedades de los límites implican operaciones que se pueden emplear con el fin de simplificar el límite de una función y convertirlos en una forma mucho más sencilla. Estas propiedades pueden utilizarse con el fin de encontrar los límites de las combinaciones de dos o más funciones o para demostrar si el límite de la función existe o no.

Cuando se trata con la combinación de dos o más funciones, por lo general, los límites de las funciones se calculan individualmente, con la ayuda de estas propiedades, y por último combinando estos con el fin de llegar al resultado final.

Estas propiedades expresan que el resultado será el mismo si el límite es tomado primero y después se realiza el álgebra o realizando el álgebra primero y luego tomando los límites.

- See more at: http://mitecnologico.com/igestion/Main/PropiedadesDeLosLimites#sthash.HsY3niTd.dpuf

UNIDAD 2: FUNCINES

Calculo Diferencial

UNIDAD 2: FUNCIONES

2.1 CONCEPTO DE VARIABLE, FUNCION, DOMINIO, CODOMINIO,

 Y RECORRIDO DE UNA FUNCION.

CONCEPTO DE VARIABLE:

Una variable es la expresión simbólica representativa de un elemento no especificado comprendido en un conjunto. Este conjunto constituido por todos los  elementos o variables, que pueden sustituirse unas a otras es el universo de variables. Existe la variable independiente (x) y la variable dependiente (y). Se le llama variable dependiente porque depende de otra variable (variable independiente).

CONCEPTO DE FUNCION:

Una función (f) es una relación entre un conjunto dado X (llamado dominio) y otro conjunto de elementos Y (llamado condominio) de forma que a cada elemento x del dominio le corresponde un único elemento f(x) del condominio (los que forman el recorrido, también llamado rango o ámbito).  En lenguaje cotidiano o más simple, diremos que las funciones matemáticas equivalen al proceso lógico común que se expresa como “depende de”.

CONCEPTO DE DOMINIO:

El dominio (conjunto de definición o conjunto de partida) de una función es el conjunto de existencia de ella misma, es decir, los valores para los cuales la función está definida. Es el conjunto 

de todos los objetos que puede transformar.

CONCEPTO DE CODOMINIO:

El condominio también llamado Intervalo o Conjunto final se le define como el grupo de resultados posibles de f(x) donde X puede variar en cualquier momento.

CONCEPTO DE RECORRIDO DE UNA FUNCION:

Es el conjunto formado por las imágenes. Son los valores que toma la función "y" variable dependiente, 

por eso se denomina f(x), su valor depende del valor que le demos a "x". En otras palabras 

los valores que puede tomar el eje "y".

2.2 FUNCION INYECTIVA, SUPRAYECTIVA Y BIYECTIVA.

FUNCION INYECTIVA:

Una función  es inyectiva si a elementos distintos del conjunto  (dominio) les corresponden elementos distintos en el conjunto  (codominio) de . Es decir, cada elemento del conjunto Y tiene a lo sumo una antiimagen en X, o lo que es lo mismo, en el conjunto X no puede haber dos o más elementos que tengan la misma imagen.

FUNCION SUPRAYECTIVA:

Una función f (de un conjunto A a otro B) es suprayectiva si para cada y en B, existe por lo 

menos un x en Aque cumple f(x) = y, en otras palabras f es suprayectiva si y sólo si f(A) = B. 

Así que cada elemento de la imagen corresponde por lo menos con un elemento del dominio.

FUNCION BIYECTIVA:

Significa inyectivo y sobreyectivo a la vez. 

Así que hay una correspondencia perfecta "uno a uno" entre los elementos de los dos conjuntos.

2.3 FUNCION REAL DE VARIABLE Y SU REPRESENTACION GRAFICA.

Cualquier función cuyo rango de conjunto incluya sólo números reales esllamada una función valorada real o simplemente una función real.

Especialmente estudiada bajo el cálculo, una función valorada real se centra en las integrales, las desigualdades en general y sus derivadas.

Una función racional, por ejemplo, cae bajo la categoría de una función valorada real.

Al igual que en cualquier otra función, tambiéna una función real pueden realizársele las operaciones básicas, tales como suma, resta, multiplicación, etc.

Aunque el denominador no sea igual a cero, la operación de división se puede realizar en tales funciones.

En el caso que k sea igual a cero la línea se superpone al eje-x.

Ejemplo, y = 12, en este caso una línea paralela al eje x que pasa por el 12vo punto formará la gráfica.

Función Identidad y Gráfico:

 Una función identidad es una función f: X → Y que tiene la propiedad f(x) = x se mantiene cierta a los elementos de X.

La gráfica de esta función es una línea recta que se traza en un ángulo de cuarenta y cinco grados con el eje x y se extiende en ambos planos negativos y positivos.

Tal función toma un elemento para sí mismo y nunca cambia su dominio. Ejemplo, f (x) = x, en este caso una línea en un ángulo de cuarenta y cinco grados pasa el eje x a travésdel origen y formará la gráfica.

Función Módulo y Gráfico:

Una función módulo o una función valorada absoluta es una de la siguiente manera, f(x) = x, f(x) = {x >= 0, -x <= 0} 

Función Recíproca y Grafico:

Una función recíproca es una como la que sigue, f(x) = 1/x, donde x <> 0 

2.4 FUNCIONES ALGEBRAICAS: FUNCION POLINOMIAL,

RACIONAL E IRRACIONAL.

FUNCION POLINOMIAL:

Es una función cuya regla esta dada por un polinomio en una variable. El grado de una función polinomial es el grado del polinomio en una variable, es decir, la potencia mas alta que aparece de x.

FUNCION RACIONAL:

Es una función que puede escribirse como cociente de dos polinomios.

FUNCION IRRACIONAL:

Es una función en cuya expresión analítica la variable independiente x aparece debajo del símbolo de raíz.

2.5 FUNCIONES TRASCENDENTES: FUNCIONES TRIGONOMETRICAS

Y FUNCIONES EXPONENCIALES.

En las funciones trascendentes la variable independiente figura como exponente, o como índice de la raíz, o se halla afectada del signo logaritmo o de cualquiera de los signos que emplea la trigonometría.

Todas las funciones que se se consideren como no algebraicas son denominadas trascendentes. Mientras tanto las funciones exponenciales, trigonométricas, logarítmicas e hiperbólicas, así como sus inversas, son funciones trascendentes.

FUNCIONES TRIGONOMETRICAS:

Cuando se usa la función f(x)= sin x, se supone que sin x significa el seno del angulo cuya medida en radianes es x. Los gráficos de las funciones seno y coseno son como las que se ilustran.

Una función trigonométrica es importante por el hecho de tener un patrón y ser repetitiva, esto le da la capacidad al que la utiliza de poder interpretar ciertos actos físicos que requieren de cierta repetitividad para funcionar. Las funciones trigonométricas mas utilizadas son: seno, coseno, tangente, cotangente, secante, cosecante.

FUNCION EXPONENCIAL:

La función exponencial es del tipo:

Sea a un número real positivo. La función que a cada número real x le hace corresponder la potencia ax se llamafunción exponencial de base a y exponente x.

EJEMPLOS:

x	y = 2x
-3	1/8
-2	1/4
-1	1/2
0	1
1	2
2	4
3	8

x	y = (½)x
-3	8
-2	4
-1	2
0	1
1	1/2
2	1/4
3	1/8

2.6 FUNCION DEFINIDA POR MAS DE UNA REGLA DE CORRESPONDENCIA, FUNCION VALOR ABSOLUTO.

Función a trozos es un nombre más general para una función que puede ser definida con la ayuda de múltiples funciones de correspondencia. Una función f: X → Y es llamadauna función a trozos si puede ser definida con la ayuda de varias funciones lineales. Podemos decir que tal función está definida en una serie de intervalos múltiples. La notación general para definir una función a trozos es la siguiente,

Como se muestra en el ejemplo, punto y coma ócomas se utilizan al final de la columna.

Sin embargo, algunos los autores prefieren usar palabras como “si” o “para” en la columna derecha, y la palabra “ de lo contrario” también se puede utilizar para indicar el caso por defecto.

La gráfica de esta función también se divide en trozos, dependiendo del número de ecuaciones que se utilicen para definir la función. Tal función es llamada de esta forma porque la definición de esta función cambia dependiendo del valor de la variable de entrada. Aquí el uso de la palabra “a trozos” se hace para describir la propiedad de esa función, que es válida para una ecuación / pieza de la función pero no en todo el dominio de la función. La función a trozos tiene una serie de funciones en su cuerpo, el dominio de cada una de ellas se define por separado. El gráfico del ejemplo dado previamente luciría de esta forma,

Es claro que el gráfico anterior contiene dos piezas separadas para indicar dos ecuaciones diferentes, por lo tanto representa la función como un todo. Un caso especial de la función a trozos es la función piso que tiene un número infinito de piezas. El valor absoluto de cualquier número es su distancia absoluta del cero, nunca es negativo dado que la distancia nunca es negativa.

Las funciones en valor absoluto se transforman en funciones a trozos, siguiendo los siguientes pasos:

1. Se iguala a cero la función, sin el valor absoluto, y se calculan sus raíces.

2. Se forman intervalos con las raíces y se evalúa el signo de cada intervalo.

3. Definimos la función a trozos, teniendo en cuenta que en los intervalos 

donde la x es negativa se cambia el signo de la función.

4. Representamos la función resultante.

1. 

D = 

2. 

D =

2.7 OPERACIONES CON FUNCIONES: CONDICION, 
MULTIPLICACION Y COMPOSICICON.

CONDICION:

Sean f y g dos funciones de variable real definidas por un mismo intervalo. Se llama suma de 

ambas funciones, y se representa por f + g.

EJEMPLO:

g(x) = x2 + 2 y

f(x) = 4x – 1

Las funciones se suman:

(g + f) (x) = (x2 + 2) + (4x – 1)

 = x2 + 4x + 1

RESTA:

(f − g)(x) = f(x) − g(x)

R:   

MULTIPLICACION:

Sean f y g dos funciones de variable real definidas por un mismo intervalo. Se llama 

multiplicación o producto de una función de f y g, y se define por:

EJEMPLO:

(f · g)(x) = f(x) · g(x)

R:  

COMPOSICION:

Dos funciones se juntan para producir un resultado, por ejemplo: f actué sobre 'x' para producir f(x) y luego g actué sobre f(x) o también llamada función composición que se representa g[f(x)].

EJEMPLO:

Ejemplo

g(x) = 2x + 3 

f(x) = -x2 + 5

 g(f(x)) = g(-x2 + 5) 

= 2(-x2 + 5) + 3

 = −2×2 + 10 + 3 

= −2×2 + 13

2.8 FUNCION INVERSA, LOGARITMICA, Y TRIGONOMETRICAS INVERSAS.

FUNCION INVERSA:

Se llama función inversa o reciproca de f a otra función f−1 que cumple que:

Si f(a) = b, entonces f⁻¹(b) = a.

Veamos un ejemplo a partir de la función f(x) = x + 4

Podemos observar que:

El dominio de f−1 es el recorrido de f.

El recorrido de f−1 es el dominio de f.

Si queremos hallar el recorrido de una función tenemos que hallar el dominio de su función inversa.

Si dos funciones son inversas su composición es la función identidad.

(f o f−1) (x) = (f−1 o f) (x) = x

EJEMPLOS: